网络流---算法理解

留言

最大流

交通网络中有人流、车流、货流，供水网络中有水流，金融网络中有金流。这些都涉及到了最大流问题

而最大流存在于网络流中

那么问题来了，什么是网络流？
  • 首先，你得有一个有向图。即网络
  • 还得有两个特殊点：起点终点。即源汇
  • 每条边有一个权值。即容量

有了这些，就构成了一个基础的网络流

有点绕。。。换个思路

自来水厂是源，家是汇

自来水厂和家之间有很多的管道用来输送水。由于地形和地质的影响，管道规格有多种。通过的水容量也各不相同

清楚了网络流，那么什么是网络流中能到达汇点的最大流呢？
  • 从源点到汇点的最大可行性流量即为最大流

这个问题就是说，自来水厂供水，那么在家能收到的最大的水流量是多少？

自来水厂开始供水之前，水流量必定是0

自开水厂开闸供水，水从管道流向家。家开始收到水

自开水厂再开一个闸门供水，水从管道流向家。家里的水流量增加

。

。

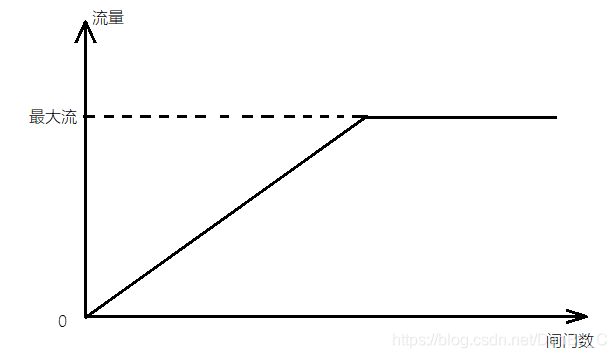
打开若干闸门，水流量持续增加

。

。

自开水厂再开一个闸门供水，水从管道流向家。家里的水流量没有发生改变
此时，便达到了从自来水厂到家这个网络的最大可行性流

网络流具有三个性质

  1. 容量限制：实际流量 < 每条边的容量

    自来水管中的水必定是小于它的最大承载容量。否则水管该爆了。

  2. 流量守恒：每一个点（不包含源汇点）到相邻节点的流量之和为0.

    每一个中间点必定是流进来多少水，流出去多少水。

    不可能没有流进来就流出去，也不可能流进来后就不出去。

    至于为什么是中间点，因为我问不用知道自来水厂的水是来自哪里的

  3. 反对称（斜对称）性：u -> v 的流量 == -（v -> u） 的流量

    在坐标系中，a 到 b 的位移是 x ，则 b 到 a 的位移是 -x

    同样的 u -> v 的流量为 f ，那么 v -> u 必定是 -f ;

网络流中的名词解释
  • 网络：有源汇点的有向图
  • 容量网络：带有容量值（权值）的有向图（不变）
  • 流量网络：带有流量值（权值）的有向图（改变），最终形态就是最大网络流
  • 残留网络: 带有残余流量值（权值）的有向图（改变），残余流量值：容量-流量的剩余量值。就像是，自来水管中，水流量没有达到管道容量时，中空气的体积容量（空的部分）。

显而易见：残留网络 = 容量网络 - 流量网络

  • 割集：割一些边，使得以源点和汇点为两边，分为两个点集。（非连通图）

  • 割：断开一些边，最小割即为断开权值最小的边

割集类似于，有小偷把自来水厂和家之间的管道偷走了一些，使得水不管从哪个管道走，都不能到家。

割则取决于小偷要偷哪个。最小割便是偷走最小，最轻的管道，最省力，最容易达到目的。